Basics
Geometric Optics
It is very fortunate for those who study gravitational lensing, that gravitational
lenses can be treated using geometric optics, for most astrophysically
relevant systems. This means solving problems in the field does not
require solving nasty tensor equations in GR. In fact, many scientists
design programs which are essentially ray tracing programs to solve complicated
gravitational systems. This fact makes may lensing problems relatively
straightforward.
Thin Screens
Of course, the central assumption of geometric optics is that the path
length of the light in the lens is much much less than the total distance
the light travels. When this assumption is satisfied, it is often
convenient to "flatten" the problem. This is done by integrating
the mass distribution serving as a lens along the line of sight, to turn
a volume mass density into a surface mass density. This surface mass
density is now a "thin screen" of mass in a well-defined plane, and it
enables us to make the problem essentially two-dimensional.
The Lens Equation
Now that we have made a number of simplifying assumptions, we can construct
what is called the lens equation. This follows from basic geometry.
If we look at this sketch:
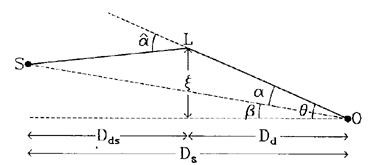
from Roger Blandford and Ramesh Narayan's 1992 ARA&A article, we
can see that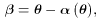 
This is the lens equation. It relates the position of the image in
the lens plane, to the position in the source plane, the distances involved
and the mass distribution of the lens.
The Einstein Radius
The lens equation defines a special angle in the lens plane, called the
Einstein Radius, when the angle in the source plane is set to zero.
This means that when the observer, lens and source are perfectly aligned,
the deflection angle is the observed angle in the lens plane. This
sets a sort of characteristic angular scale for any gravitational lensing
problem. As previously mentioned, for other stars in our galaxy,
this angle is generally ~1 milliarcsecond. However, for galaxy or
cluster lensing it is more like ~1-a few arcseconds.
Magnification
Since gravitational lensing preserves surface brightness (luminosity per
unit area), but increases the size of objects, gravitationally lensed objects
can be enormously brightened. As a result, we can often see intrinsically
dimmer galaxies that we would not have seen if they had not been lensed.
Also in lensed galaxies, we can resolve smaller structures, since they
have been enlarged by the lens.
Critical Lines / Caustics
Critical lines are the contours which can be drawn on a mass sheet in the
lens plane, which enclose an average "critical surface mass density".
This critical density represents the dividing line between single and multiple
images (more below). When this contour is transformed into the source
plane (using the lens equation), the path it traces out in the source plane
is called a caustic.
Multiple Images
Different lens geometries can produce some interesting image geometries.
As has already been mentioned, sometimes a lens will produce two
images of a source (the first QSO lensing discovery). It can also
produce four
images, a configuration known as an Einstein Cross. Or, if the lens,
source and observer are perfectly aligned, we will see an Einstein
Ring (at an angle given by the Einstein Radius).
Time Delay
If one has multiple images of a time varying source, a time delay between
the arrival time of the events in each image at the location of the observer
is apparent. This is caused by two effects. The first is a
simple path length difference. The light from both images is travelling
at speed c, but unless the images are perfectly aligned, one signal travelled
a shorter distance than the other, so one signal will arrive before the
other. The second effect which comes into play is gravitational time
dilation. This refers to the fact that clocks run slower in a gravitational
potential well (another consequence of general relativity). So the
light ray which passes deeper in the potential well will have slowed down.
These two effects tend to partially cancel each other, but since they have
different functional forms, they can be separated in theoretical work and
modelled in real systems. The measured time delay can thus tell us
a lot about a lens.