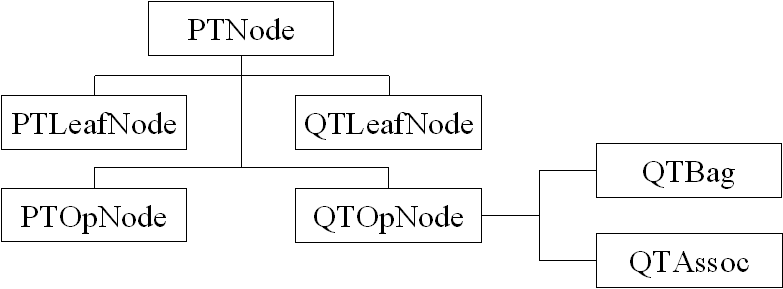

The Base class for both Trees is the PTNode abstract class. The Class diagram looks like the following:

The lines represent inheritance. All classes inherit from PTNode, and QTBag and QTAssoc inherit from QTOpNode. This design makes it easy to convert PTNodes to QTNodes. This conversion is needed at the inefficient OR treatment (see Section 6.3) The OpNodes have an array of children (of PTNode type) and the LeafNodes have a "content" data member.
There is a cross-reference to the IndexMap class and the Intersection class discussed below.
The IndexMap class encorporates the Sky Index, all Flux Indices, the Partition Map and all the necessary masks for the Sky Bits. We have 3 data members:
The Intersection class has 4 IndexISect classes as data members, as discussed in Section 6.2. The IndexISect class consists of

There are well-defined logical operations on Itersection and IndexISect.
To geometrically represent queries in the multidimensional flux space a linear combination query can be viewed as a hyperplane in the flux space. A hyperplane can be represented with a sxFluxConstraint object. The logical AND combination of hyperplanes results a convex polyhedron, it is represented by the sxFluxConvex class. Logical OR combination of convexes gives a so called domain, which is a union of convexes. It is represented by an sxFluxDomain. The most important functionality of these classes to detect an intersection with a hypercube (a bounding box of the sxFluxIndex).
sxFluxConstraint represents a linear combination query in the form:
aCoeff[0]*aFlux[0] + aCoeff[1]*aFlux[1] ... + aCoeff[gNumFluxes+1] > 0
Exact equation is not allowed, since because of the errors it has zero measure.
The observed object's distribution covers mostly a compact region of
the flux space. These are the regular objects. Due to measurement error
or objects those are not ordinary stars or galaxies (like meteor traces,
asteroids, ufos) there are measured objects outside of this region. These
are outliers. Since they span a large region of the flux space they can
make bounding boxes useless. That's why they are stored separately. The
query can be run on either of, or both of these objects. It is like a new
dimension (but only with values 0 and 1) added to to the flux dimensions.
The BitList class is an array of bits with efficient logical operations
defined on it. There is a compress(stream) and decompress(stream) method
to compress itself out on a stream. A PCX-like compression is used. The
scheme is the following:
We do a byte-encoding, and write those bytes out in hex form (2 letters
for each byte). The first bit (128) of each byte denotes whether the byte
contains
actual data or a count of bits.
If the first bit is 0, the next 7 bits are data-bits.
If the first bit is 1, the next bit (64) is the value and the 6 last
bits give the count (0-63). It does not make sense to count 0 times so
bits are only counted if there are at least 8 bits with the same value.
So the count is 8-71. For more than 71 bits, the next byte is taken. The
byte is then written out to the stream as a hex number.
This compression results in a 14% blowup in size for the worst case (i.e. BitList consists of 01010101...) and in a compression factor of 71 for the best case (all bits alike). Example: a series of 0101's of size 92 compresses into
2A552A552A552A552A552A552A.101
a series of 1111's of size 92 compresses into
FFCD.00
The dot and the value following it indicates how many bits are in the last byte, if any, and then the last bytes follows in hex. In the above example, .101 means only a single bit=true. In this way the exact size of the BitList can be restored, not just chunks of 7.
The BitListIterator class provides an efficient way to iterate through the BitList. see the methods of it for details.